LIAISONS CHIMIQUES - Liaison et classification

LIAISONS CHIMIQUES - Liaison et classification

Le problème de la nature de la liaison chimique s’est posé dès que fut entrevue la structure discontinue de la matière. Depuis l’Antiquité, chaque époque s’y est intéressée, proposant des solutions adaptées à ses connaissances. Démocrite munissait les particules de petits crochets afin de leur permettre de se lier entre elles. Le Moyen Âge, abandonnant une description aussi simpliste, introduisit la notion d’affinité, simple transposition des sentiments humains sans grand rapport avec la réalité.

Il fallut attendre la fin du XVIII^e siècle pour que soit tentée la première ébauche de théorie physique avec Laplace, qui essaya d’utiliser les lois de la gravitation récemment mises en évidence. La découverte de l’électrolyse (H. Davy, 1806) amena à identifier l’affinité entre les particules à une attraction entre charges électriques. J. J. Berzelius (1812) pensait que les atomes possédaient deux pôles électriques de signes opposés, expliquant ainsi la possibilité d’associations par interaction électrostatique. Cependant, à cette théorie s’opposa bientôt celle de J.-B. Dumas (1834), qui, au contraire, considérait que la molécule formait un tout, les atomes ayant perdu toute individualité dans celle-ci; de là vint la notion de radicaux susceptibles de s’échanger au cours des réactions. La théorie de Dumas s’appliquait essentiellement aux composés organiques, non électrolysables, alors que celle de Berzelius, qui connut un regain de faveur à la suite des travaux de S. Arrhenius sur la dissociation des molécules en ions, paraissait mieux s’adapter aux composés minéraux. A. G. Werner (1892) découvrit la possibilité pour des ions de s’associer entre eux et de former de véritables molécules au sens de Dumas. De cet ensemble de faits assez confus résulta finalement l’idée de l’existence de plusieurs modes de liaisons totalement différents.

Lorsque la structure de l’atome fut élucidée, peu après 1900, le retour aux théories électriques s’imposait. Il était désormais hors de doute que les liaisons entre les atomes étaient assurées par l’intermédiaire des électrons (K. Starke, R. G. Parsons, 1915). W. Kossel (1916) développa une théorie fondée sur l’interaction électrostatique des ions dans les cristaux. Mais cette théorie se prêtait mal à une application aux molécules isolées, et en particulier lorsqu’elles étaient symétriques comme H² ou Cl².

Parallèlement, G. N. Lewis (1913) proposait un mode de liaison nouveau, la covalence, modèle perfectionné plus tard par I. Langmuir. Pour Lewis, la liaison était assurée par la mise en commun d’électrons entre les atomes avec formation de paires, le nombre de paires entourant les atomes étant limité à huit (règle de l’octet). Bien qu’assez proche de la réalité, cette ingénieuse théorie ne reposait sur aucun support théorique au moment où elle fut proposée. En conclusion, au début de ce siècle, la question de la nature de la liaison chimique restait entière. La multiplicité des explications proposées était la condamnation même de toutes ces interprétations, puisque la liaison chimique est en fait unique.

L’élaboration par Louis de Broglie, en 1924, de la mécanique ondulatoire éclaira d’un jour nouveau le problème. On savait désormais que la physique classique ne s’appliquait pas à l’infiniment petit, mais qu’il fallait faire appel à un autre formalisme. Le problème de l’atome d’hydrogène fut traité avec succès par E. Schrödinger dès 1926 et, aussitôt après, en 1927, W. Heitler et F. London, utilisant ces résultats, rendirent compte de la stabilité de la molécule H². Ce mémoire fondamental ouvrit une voie nouvelle: la chimie théorique. Appuyée sur une base mathématique solide, la théorie de la liaison chimique n’a cessé depuis lors de se développer avec succès, si bien qu’aujourd’hui on peut considérer le problème comme résolu dans son principe, les seules difficultés étant d’ordre purement algébrique ou même simplement numérique.

1. Fondements de la théorie moderne

Principes de la mécanique quantique

La description de l’état d’une particule, en mécanique quantique, se réduit à la seule connaissance d’une fonction 切 des coordonnées et du temps, dite fonction d’onde. Cette fonction n’a pas de sens physique en elle-même, mais le carré de son module représente la probabilité de trouver à l’instant t les particules aux points de coordonnées correspondantes. Tout se passe comme si les particules avaient perdu leur individualité pour être remplacées par un nuage continu de densité | 切|².

La fonction 切 est solution d’une équation aux dérivées partielles, dite équation de Schrödinger. Dans le cas d’un système isolé, l’énergie reste constante et la fonction 切 se décompose en un produit d’une fonction d’espace 祥, ne portant que sur les coordonnées des particules, et d’une fonction du temps, telle que la probabilité | 祥|² reste constante au cours du temps et égale à | 切|². On dit que le système est dans un état stationnaire. La fonction d’espace 祥 est solution d’une équation plus simple qui s’écrit symboliquement: H 祥 = E 祥, E désignant l’énergie du système et H un opérateur différentiel appelé hamiltonien. Schrödinger a formulé les règles de construction de cet opérateur.

L’étude mathématique des solutions de l’équation de Schrödinger montre que l’énergie ne peut pas prendre des valeurs arbitraires, ce qui se traduit par l’existence de niveaux énergétiques discrets. Les valeurs de l’énergie fournissant des solutions acceptables sont appelées valeurs propres de l’opérateur hamiltonien, et les fonctions d’onde correspondantes, fonctions propres. On démontre que ces fonctions sont orthogonales entre elles.

De plus, la théorie prévoit, en accord avec l’expérience, que, pour décrire complètement une particule, il faut lui adjoindre une coordonnée supplémentaire dite de spin. Cette dernière n’a pas d’équivalent classique, et il serait erroné d’essayer de chercher à lui donner une représentation élémentaire. Pratiquement, la fonction d’onde associée à une particule est le produit de la fonction d’espace, définie plus haut, par la fonction de spin. Cette dernière, comme la fonction d’espace, est fonction propre d’un certain opérateur. Pour un électron, cet opérateur ne possède que deux fonctions propres, notées en général 見 et 廓, et correspondant à des valeurs propres opposées.

Enfin, les fonctions électroniques sont antisymétriques par rapport à l’échange des électrons. Cette propriété a pour conséquence que deux électrons d’un système donné ne peuvent avoir toutes leurs caractéristiques identiques. Car, s’il en était ainsi, l’échange de ces deux électrons laisserait la fonction inaltérée (principe de Pauli).

Structures des atomes

On sait, depuis les expériences de E. Rutherford (1909), qu’un atome est constitué par des électrons de charge négative (face=F0019 漣 e ) gravitant autour d’un noyau de charge positive, multiple de celle de l’électron (+ Ze ) et de masse très supérieure, de sorte que, pratiquement, le problème se ramène au mouvement des seuls électrons autour de la charge nucléaire immobile.

L’intégration de l’équation de Schrödinger relative à l’atome le plus simple, celui de l’hydrogène ou des ions hydrogénoïdes (He²⁺, Li ³⁺, etc.), qui ne possèdent qu’un seul électron, est possible rigoureusement et fournit, pour les états stationnaires, des solutions qui se groupent, par familles d’énergie: 漣 Z ²/(2 n ²) (où n est un entier positif), en unités atomiques:

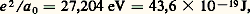a ⁰ étant l’unité de longueur connue sous le nom de rayon de Bohr, égale à 0,052 93 nm.

Pour n = 1, on a une fonction de symétrie sphérique, que l’on notera 1 s . Elle correspond à une densité électronique également sphérique. Pour n = 2, on a une fonction de symétrie sphérique 2s et trois fonctions, notées 2 p , de même nature entre elles et possédant chacune un axe de révolution. Les trois axes forment un trièdre trirectangle. On nommera ces fonctions: 2 p ^x , 2 p ^y et 2 p ^z , en indiquant l’axe en indice. Chaque fonction est antisymétrique par rapport au plan perpendiculaire à l’axe et passant par le noyau, ce qui entraîne que la densité est nulle dans ce plan et symétrique par rapport à ce plan hors de celui-ci.

Pour n = 3, on a une fonction de symétrie sphérique (3 s ), trois fonctions de type p : (3 p ), et cinq fonctions de structure plus complexe: 3 d .

D’une façon générale, on obtient, pour la famille d’énergie 漣 Z ²/(2 n ²), n ² fonctions d’onde. Ces fonctions sont appelées orbitales atomiques . L’ensemble des orbitales correspondant à la même valeur de n forme une couche .

Le problème d’un atome quelconque contenant plusieurs électrons peut être envisagé comme une généralisation de celui de l’hydrogène. En effet, si on considère un électron donné, il est soumis à l’attraction du noyau et à la répulsion des autres électrons. En l’absence de champ électrique ou magnétique extérieur, aucune direction de l’espace n’est particularisée, si bien que le potentiel moyen auquel est soumis chaque électron est de symétrie sphérique. Tout se passe pour lui comme si la charge nucléaire centrale Z était diminuée à cause de l’effet d’écran causé par les autres électrons. Chaque électron peut donc être décrit par une fonction d’onde analogue aux orbitales atomiques de l’hydrogène, mais caractérisée par une charge nucléaire convenable. J. Slater a donné des règles simples pour calculer ces charges.

Une différence essentielle cependant est à noter. Alors que, dans l’atome d’hydrogène, les orbitales se groupent par familles de même énergie déterminée par le nombre n et comprenant n ² fonctions, ici les diverses orbitales d’une même couche se subdivisent en niveaux. Par ordre d’énergie croissante à l’intérieur d’une couche donnée, on trouve successivement (lorsqu’ils existent) le niveau s , les trois niveaux p confondus, les cinq niveaux d confondus, etc. Cet éclatement des composantes des diverses couches entraîne un enchevêtrement des niveaux relatifs à des couches différentes. Par exemple, on a la succession: 4 s 麗 3 d 麗 4 p , les différences d’énergie étant faibles.

Dans l’état de plus basse énergie, les électrons de l’atome tendent à se placer sur les niveaux les plus bas, à raison de deux au maximum par niveau. En effet, à une fonction d’espace donnée, on ne peut associer que deux fonctions de spin, correspondant à des valeurs propres opposées. On dit que les électrons forment des paires de spins antiparallèles. Nous laisserons de côté le cas d’un remplissage incomplet.

2. Méthodes d’étude des molécules

La molécule d’hydrogène

La molécule H² est la plus simple des molécules neutres puisqu’elle résulte de l’union de deux atomes d’hydrogène. Malheureusement, l’équation de Schrödinger correspondante n’est pas intégrable, aussi des solutions approchées doivent-elles être recherchées.

La première tentative fut celle de Heitler et London. Ces auteurs supposèrent que les électrons (1 et 2) utilisent les orbitales 1 s nommées a et b des atomes d’hydrogène A et B. Afin de respecter la symétrie entre les électrons 1 et 2 d’une part, et les noyaux d’autre part, Heitler et London postulèrent pour fonction d’espace les combinaisons:

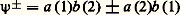(à une constante près) qui laissent la densité électronique invariante dans les échanges entre électrons et entre noyaux. Dans cette formule, a (1) signifie que les coordonnées d’espace entrant dans l’expression de l’orbitale atomique 1 s de l’atome A, sont celles de l’électron 1. À partir de cette fonction, on peut calculer l’énergie associée à un état stationnaire:

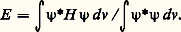La valeur de l’énergie E ainsi obtenue dépend seulement de la distance internucléaire R , puisque les fonctions a et b sont connues. L’énergie apparaît comme la somme de deux termes: l’énergie des atomes isolés et un terme correctif E ^l , dû à l’interaction entre les atomes. La figure 1 montre l’allure de la variation de ce dernier terme en fonction de R pour les deux fonctions 祥⁺ et 祥^- (fig. 1).

Pour 祥^-, E ^l est toujours positif, l’énergie de l’ensemble est supérieure à celle des atomes isolés: l’édifice formé par les deux atomes est instable. Pour 祥⁺, au contraire, E ^l , positif pour les courtes distances, devient négatif, l’ensemble étant alors plus stable que les atomes isolés. De plus, l’énergie passe par un minimum pour une certaine distance R⁰. Une modification de la distance à partir de cette valeur entraîne, dans tous les cas, une augmentation de l’énergie, donc une perte de stabilité. La distance R⁰ correspond par conséquent à une position d’équilibre stable. On dit qu’il y a liaison chimique, la valeur absolue de E ^l correspondante est l’énergie de liaison.

Pour achever la description du système, il faut tenir compte des coordonnées de spin. Les fonctions d’onde électroniques devant être antisymétriques par rapport à l’échange des électrons, à la fonction d’espace 祥⁺, symétrique, doit nécessairement être associée une fonction de spin antisymétrique. Celle-ci est unique et s’écrit à un facteur près:

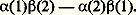Ce qui montre que les deux électrons ont formé une paire, mettant leurs spins antiparallèles.

Non seulement le calcul rend compte qualitativement de l’existence de la molécule H², mais il fournit aussi des ordres de grandeur tout à fait acceptables pour les caractéristiques de celle-ci: 0,080 nm pour la distance d’équilibre et 301 kJ.mol^-1 pour l’énergie de liaison. Expérimentalement, la distance d’équilibre est 0,074 nm, et l’énergie 454,3 kJ.mol^-1. Le désaccord provient du fait qu’on a utilisé pour 祥 une expression approchée. De nombreux travaux ont été faits pour améliorer la description du système, modifiant soit la forme de la fonction postulée, soit les orbitales atomiques de base a et b , soit les deux à la fois, aboutissant à un accord remarquable avec l’expérience. Mais un fait important est à souligner, quelle que soit la méthode utilisée: l’existence de la molécule H² et sa stabilité résultent de la formation d’une paire d’électrons, ce qui justifie l’interprétation de Lewis. C’est ce que veut représenter le tiret qui unit les symboles atomiques dans l’écriture classique: H 漣 H.

Méthode des paires

Généralisant le résultat obtenu pour H², on peut construire une suite de fonctions polyélectroniques 祥ⁱ correspondant aux diverses façons d’associer les électrons par paires dans la molécule. Ces fonctions sont des solutions approchées de l’équation de Schrödinger. Pour obtenir une solution améliorée, on forme des combinaisons linéaires des 祥ⁱ , de façon à minimiser l’énergie (cf. biochimie et chimie QUANTIQUE). L. Pauling et J. Slater ont indiqué un procédé systématique pour construire les fonctions de base 祥ⁱ en s’aidant de schémas chimiques. Par exemple, pour la molécule H², on utilisera les fonctions correspondant aux trois structures: H 漣 H, H⁺H^- et H^-H⁺. Dans la première forme, la paire d’électrons est répartie symétriquement entre les deux atomes comme dans le schéma de Lewis, d’où le nom de forme covalente qu’on lui donne, alors que les deux autres sont dites ioniques par analogies avec le schéma électrostatique de Kossel. Ces schémas de base sont appelés formes canoniques. La fonction 祥 finale qui représentera le système sera une combinaison linéaire des fonctions 祥ⁱ associées à chaque forme canonique. La molécule sera donc décrite par une fonction intermédiaire entre les fonctions de base, d’où le nom de structure mésomère donné à la structure réelle de la molécule (du grec 猪﨎靖礼﨟, intermédiaire) et le nom de mésomérie donné à la méthode. On note aussi:

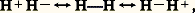reliant les diverses formes canoniques par le symbole 良轢, qui ne doit pas être confondu avec celui qui indique un équilibre chimique (face=F0019 燎), car les formes canoniques n’ont aucune existence réelle et ne sont que des artifices de calcul. Seule la fonction finale 祥 a un sens. En particulier, il est incorrect de raisonner sur l’une ou l’autre de ces formes pour rendre compte des propriétés chimiques. Toutefois, le nombre des fonctions 祥ⁱ possible est très élevé (plus de 4 600 000 pour l’ion S^2-4), de sorte qu’on se borne aux schémas chimiquement les plus probables.

Partant de l’idée que la liaison est assurée par des paires d’électrons localisées entre couples de noyaux, la mésomérie conduit à une conception beaucoup plus floue des liaisons, la molécule n’étant finalement représentable par aucun schéma chimique.

Méthode des orbitales moléculaires

La méthode des orbitales moléculaires pose a priori pour fonction d’onde totale un déterminant de Slater (fig. 2) construit sur des fonctions d’espace 﨏 monoélectroniques. Au voisinage de chaque noyau, le champ agissant sur un électron dans une molécule est pratiquement le même que dans l’atome correspondant isolé, si bien que, localement, les diverses orbitales atomiques constituent des solutions approchées de l’équation de Schrödinger relative à la molécule. On cherchera donc, pour fonction d’espace, des combinaisons linéaires des orbitales atomiques 﨑^r des atomes de la molécule:

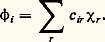D’où le nom de L.C.A.O. (Linear Combinations of Atomic Orbitals ) donné aussi à la méthode. Ces fonctions qui généralisent les orbitales de l’atome sont appelées ortibales moléculaires . Le remplissage des divers niveaux obtenus se fera de la même façon que dans les atomes: dans l’état le plus stable, les électrons se placeront par paires de spins antiparallèles sur les orbitales moléculaires de plus basse énergie.

Les coefficients c ^ir se déterminent en écrivant que l’énergie associée à la fonction 祥 (1, 2, ..., n ) est minimale. D’une façon générale, si l’on introduit m fonctions atomiques 﨑, on obtient m orbitales moléculaires. Si le nombre d’électrons n est pair, on aura n /2 niveaux doublement occupés et m 漣 n /2 vides. Les niveaux moléculaires correspondant à une stabilisation énergétique par rapport aux orbitales atomiques isolées sont dits liants et ceux qui correspondent à un système moins stable antiliants .

En principe, le calcul des orbitales moléculaires doit se faire sur une base d’orbitales atomiques aussi étendue que possible, mais en pratique on peut se contenter de faire intervenir les orbitales des niveaux supérieurs occupés dans les atomes, laissant en particulier les électrons des couches internes localisés autour des noyaux. Par exemple, pour l’atome de carbone, les fonctions de liaisons seront construites sur les orbitales 2 s et 2 p seulement. Les électrons correspondants seront dits périphériques ou encore de valence .

De plus, ne se combinent pratiquement entre elles que des orbitales qui possèdent un domaine commun de densité électronique appréciable.

Hybridation des orbitales atomiques

La méthode des orbitales moléculaires conduit à des fonctions portant sur toutes les orbitales atomiques introduites, fournissant ainsi en général une densité électronique répandue sur toute la molécule. La description qui en résulte ne se prête pas à une représentation élémentaire utilisable pour le chimiste. Les fonctions 﨏 n’étant déterminées qu’à une transformation unitaire près (cf. chimie QUANTIQUE), on peut remplacer ces fonctions par des combinaisons fournissant des densités localisées entre les noyaux selon la conception du chimiste. Mais il revient au même, comme la base des orbitales atomiques n’a rien d’imposé, de remplacer les orbitales des atomes par des combinaisons linéaires orthogonales, reflétant la structure générale de la molécule et ses symétries. Une telle opération porte le nom d’hybridation des orbitales.

Les fonctions ainsi obtenues ont l’avantage de fournir des densités électroniques très dissymétriques par rapport aux noyaux, concentrées dans un domaine restreint, contrairement aux orbitales de départ. Cela permet de définir une direction principale, correspondant à ce maximum de probabilité de présence de l’électron. Les fonctions moléculaires qui en résultent sont construites sur des couples d’orbitales hybrides ayant un domaine de densité importante commun et la densité électronique corresondante est localisée entre les noyaux. Par exemple, pour l’atome de carbone dans la molécule de méthane CH⁴, on remplace les orbitales (2 s ), (2 p ^x ), (2 p ^y ), (2 p ^z ) de nature différente par les quatre combinaisons orthogonales:

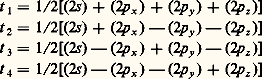qui correspondent à des orbitales de même nature, se déduisant l’une de l’autre par une rotation autour des noyaux, donc de même symétrie que l’édifice CH⁴. Les directions principales de ces orbitales forment, dans le cas présent, un faisceau régulier à 109,5⁰. Les atomes d’hydrogène viennent se placer sur ces directions principales pour former quatre liaisons C 漣 H, disposées à 109,5⁰ l’une de l’autre, avec une forte concentration électronique entre les noyaux. Ainsi apparaît le lien entre l’hybridation des orbitales atomiques, opération essentiellement mathématique, et la notion de valence dirigée sur laquelle est bâtie la stéréochimie classique.

Plusieurs types d’hybridation sont à envisager selon l’environnement de l’atome. On s’intéressera d’abord au cas le plus simple, celui où les hybrides sont construites seulement sur les orbitales s et p . Si l’atome est lié à quatre atomes répartis dans l’espace, les directions principales forment un faisceau, régulier si les quatre hybrides sont de même nature comme dans le méthane, irrégulier si elles sont différentes. Dans tous les cas, elles portent sur l’orbitale s et les trois orbitales p : l’hybridation est dite sp ³, symétrique ou non. Si l’atome est lié à trois atomes seulement et s’il est situé dans leur plan, on démontre que l’on a trois orbitales hybrides construites sur l’orbitale s et sur deux orbitales p , et dont les directions principales sont situées dans le plan des noyaux. La troisième orbitale p reste pure, c’est-à-dire non hybridée. Son axe est perpendiculaire au plan des noyaux. L’hybridation est dite sp ², symétrique ou non. Enfin, si l’atome n’est lié qu’à deux autres atomes et s’il est aligné avec eux, l’hybridation ne porte plus que sur l’orbitale s et une orbitale p , laissant les deux autres orbitales p pures. L’hybridation est dite sp , symétrique ou non.

L’utilisation d’orbitales d conduit à des structures plus complexes. Les plus usuelles sont: sp ³d ², fournissant six directions principales, et sp ³d , cinq. Dans le premier cas, on peut obtenir jusqu’à six orbitales identiques, leurs directions principales étant alors situées suivant les demi-axes d’un trièdre trirectangle; dans le second cas, la disposition la plus symétrique fournit trois orbitales de directions principales coplanaires et disposées à 120⁰ l’une de l’autre, et deux orbitales pointant dans des directions principales opposées, perpendiculaires au plan des premières (fig. 3).

3. Classification structurale des molécules

La notion d’hybridation permet une classification rationnelle des divers types structuraux. On se bornera aux plus simples.

Hybridation sp³

L’hybridation sp ³ se rencontre en particulier avec les éléments de la seconde ligne de la classification périodique. Ces atomes, ayant à leur disposition une orbitale s et trois orbitales p , on pourra, à partir de celles-ci, former quatre hybrides, si bien qu’au maximum ces atomes pourront se lier à quatre atomes. Le cas le plus simple est celui du carbone, qui possède quatre électrons périphériques, c’est-à-dire que chaque orbitale a à sa disposition un électron qui sera susceptible de se lier à un électron de l’atome qui lui sera offert, formant ainsi une paire assurant une liaison, par exemple, dans le méthane (CH⁴), où l’hybridation est sp ³, symétrique à cause de l’équivalence des atomes d’hydrogène.

Si le nombre d’électrons périphériques est supérieur à quatre, il y aura nécessairement formation de paires d’électrons non liants, localisées sur des orbitales hybrides, abaissant d’autant le nombre de liaisons. Ainsi, pour l’azote, qui possède cinq électrons périphériques, on aura une paire et trois liaisons, comme dans l’amoniac (NH³); pour l’oxygène, deux paires et deux liaisons (OH²); pour le fluor, trois paires et une liaison (FH).

Les paires libres peuvent fixer un proton H⁺ qui ne possède aucun électron, formant ainsi une liaison NH³ + H⁺NH⁴⁺, l’ion ammonium, symétrique, a une structure analogue à celle du méthane. Avec l’eau, on obtient de même l’ion OH³⁺ de structure analogue à celle de l’ammoniac.

Ces phénomènes avaient donné lieu jadis à l’introduction d’un mode de liaison spécial, la liaison semi-polaire , qui était notée, par exemple, H³NH⁺. Une telle représentation est à rejeter, car elle laisserait croire qu’une des quatre liaisons NH est différente des autres. D’autre part, le mécanisme de formation de cette liaison ne se distingue en rien du mécanisme général, à savoir la mise en commun d’une paire d’électrons de spins antiparallèles sur un niveau moléculaire.

On peut aussi avoir des systèmes condensés en soudant entre eux des atomes sp ³, par exemple dans l’éthane H³C 漣 CH³, obtenu (formellement au moins) à partir de deux groupements CH³, porteurs chacun d’une orbitale hybride occupée par un électron.

Dans tous les cas qui viennent d’être envisagés, les liaisons sont localisées entre les atomes, et la densité électronique est pratiquement de révolution autour de la ligne des noyaux correspondante. Elles sont nommées 諸 ou simples liaisons.

Hybridation sp²

L’hybridation sp ² se rencontre dans les molécules planes, comme l’éthylène C²H⁴. Les orbitales hybrides sont utilisées pour former des liaisons de type 諸 entre les carbones et les hydrogènes. Mais en plus, sur chaque atome de carbone, il reste un électron décrit par une orbitale 2 p pure. Ces électrons forment une paire qui se place sur un niveau moléculaire construit sur les deux orbitales atomiques 2 p . Pour les orbitales atomiques des atomes d’hydrogène et celles, hybrides, des carbones, le plan de la molécule est plan de symétrie, alors que, pour les orbitales p pures, il est plan d’antisymétrie. Il en résulte deux classes d’orbitales moléculaires, celles, symétriques par rapport au plan des noyaux et dites 靖, qui correspondent aux liaisons C 漣 H et C 漣 C de type 諸, et celles, antisymétriques par rapport à ce plan et dites 神, qui correspondent à la paire supplémentaire et sont, par conséquent, construites sur les orbitales 2 p pures.

La liaison entre les carbones est donc assurée au total par deux paires d’électrons, c’est une double liaison , que l’on représente par le symbole C = C. Une telle liaison est plus courte que la simple liaison correspondante C 漣 C: 0,133 nm contre 0,154 nm dans l’éthane. La fonction 神, qui correspond à des orbitales ne pointant pas l’une vers l’autre, c’est-à-dire ne possédant pas un domaine de forte densité électronique commun, est moins stable que les liaisons 諸 du système 靖, ce qui explique que les molécules possédant de tels systèmes puissent fixer des atomes d’hydrogène ou d’halogènes pour n’avoir plus que des liaisons 諸, plus stables, avec une hybridation sp ³. On dit qu’elles sont insaturées .

Analogue est la structure du groupement carbonyle C = O. Toutefois, alors que, dans l’éthylène, par raison de symétrie, le plan médiateur du segment CC est plan de symétrie pour la densité électronique, ici la nature différente des atomes, donc des orbitales p , fait apparaître une dissymétrie dans le nuage électronique qui sera déplacé vers l’atome d’oxygène.

Si une molécule plane possède plusieurs systèmes insaturés adjacents, comme le butadiène:

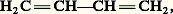les fonctions d’onde de la classe 神 sont construites sur l’ensemble des orbitales p non hybridées. Les axes de ces orbitales étant parallèles, chaque orbitale se trouve par rapport à ses voisines immédiates dans une situation comparable, on n’a pas ici de domaine de forte densité commun, si bien que la densité électronique relative à chaque paire d’électrons n’est pas localisée entre deux atomes, mais répandue sur l’ensemble de la molécule. Les doubles liaisons, ou plutôt les systèmes 神 des doubles liaisons du schéma classique ne sont plus indépendants, mais conjugués (cf. RÉSONANCE [Chimie]). Par conséquent, la liaison entre les deux carbones centraux du butadiène est assurée, non seulement par la paire 諸 de la classe 靖, mais aussi par une certaine fraction d’électrons provenant de la délocalisation des systèmes 神. On dira qu’elle a un caractère intermédiaire entre une simple et une double liaison. La théorie permet de préciser sa nature par un nombre, l’indice de liaison, et en particulier de déterminer sa longueur, qui est comprise entre celles de la simple et de la double liaison. Dans le cadre de la méthode des orbitales moléculaires, l’indice de liaison 神 est donné par:

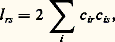si l’on utilise des orbitales atomiques de base 﨑^r et 﨑^s orthogonales. Pour l’éthylène, cet indice vaut 1; on ajoutera 1 à l’indice 神 pour avoir l’indice total 靖 + 神, ce qui donnera 2 pour une double liaison isolée. Dans le butadiène, l’indice 神 relatif à la liaison centrale se situe aux environs de 0,3, alors que celui des liaisons terminales est à peine inférieure à 1, ce qui correspond à un net raccourcissement pour la liaison centrale (0,147 nm contre 0,152 nm s’il n’y avait pas de liaison 神), alors que les liaisons terminales ne sont pratiquement pas affectées (0,134 nm). Dans le benzène, où la conjugaison porte sur trois liaisons doubles, l’effet est encore plus marqué: toutes les liaisons sont égales (indice 神: 2/3; longueur: 0,140 nm); cette uniformatisation des liaisons entraîne des conséquences importantes du point de vue chimique, connues sous le nom d’aromaticité ^{[cf. AROMATICITÉ]}.

Hybridation sp

L’hybridation sp apparaît dans les molécules linéaires, comme l’acétylène C²H². La liaison entre les deux carbones est assurée par une liaison de type 諸 et deux liaisons de type 神 : 神 et 神 , dont les axes des orbitales sont situés dans des plans rectangulaires. C’est une triple liaison notée C 令 C. Elle est encore plus courte que la double 0,12 nm.

Comme avec les systèmes sp ², il peut y avoir conjugaison, par exemple dans le diacétylène HC 令 C 漣 C 令 CH, où les liaisons terminales sont légèrement affaiblies et la liaison centrale renforcée. On définit un indice global 神 + 神 , qui vaut 2 pour l’acétylène, ce qui donne, en ajoutant 1 pour la liaison 諸, 3 au total.

Hybridation sp³d

Avec les éléments de la troisième ligne, à côté des hybridations portant sur les orbitales 3 s et 3 p , identiques aux précédentes (comme dans PH³, SH²), on rencontre des édifices utilisant des orbitales 3 d , PCl⁵ par exemple. La molécule est formée de trois liaisons égales, à 120⁰ dans un plan, et de deux liaisons de nature différente, mais égales entre elles, d’axe perpendiculaire au plan des premières. L’utilisation d’une orbitale 3 d , située énergétiquement bien au-dessus des niveaux 3 s et 3 p , nécessite un apport extérieur d’énergie, si bien que, parmi les édifices de type MX⁵, seuls ceux pour lesquels la formation des liaisons MX apportera une forte stabilisation pourront exister. Le cas des halogénures de phosphore est particulièrement net: PF⁵ est stable, PCl⁵ se dissocie facilement en Cl² et PCl³ avec retour à l’hybridation sp ³, PBr⁵ est dissocié dès la température ordinaire, PI⁵ n’existe pas.

Les éléments de la même colonne (Sb, Bi) donnent des structures analogues avec les halogènes ou les groupements OH.

Hybridation sp³d²

Les éléments de la troisième ligne peuvent entrer dans les molécules avec une hybridation sp ³d ²: SF⁶, (SiF⁶)^2-, mais c’est surtout avec les éléments de transition que l’on rencontre cette structure. Les niveaux 3 d s’intercalant entre les 4 s et 4 p , eux-mêmes très voisins, une hybridation portant sur l’ensemble de ces orbitales est énergétiquement très facile et conduit à des composés stables. Les molécules obtenues sont de type MX⁶, où X est un atome, un ion ou une molécule, porteur d’une paire d’électrons libres. Il y a formation de six liaisons de type 諸; les électrons provenant des niveaux périphériques (4 s , 3 d , 4 p ) de l’atome central se répartissent soit sur les trois niveaux atomiques 3 d non utilisés et sur les niveaux moléculaires antiliants 諸 qui correspondent aux six liaisons M 漣 X, soit sur des niveaux moléculaires, si une conjugaison peut s’établir entre les 3 d non hybridés et les groupements X. [Co(NH³)⁶]³⁺ est un exemple du premier cas, et [Co(CN)⁶]^3- un exemple du second. Comme pour l’hybridation sp ³, si le nombre d’électrons est trop élevé, des paires libres remplaceront des groupements X. De plus, on pourra, avec des groupements différents, obtenir des hybridations dissymétriques.

Hybridations mixtes

Plusieurs types d’hybridation peuvent se rencontrer dans une même molécule, par exemple dans le propène H²C 略CH 漣CH³ ou le vinylacétylène H²C 略CH 漣C 令CH. En toute rigueur, dans de tels édifices, les symétries des fonctions d’onde sont celles de l’ensemble de la molécule. Par exemple, pour le propène, molécule non plane, il n’y a plus de système 靖 ou 神. Cependant, l’interaction entre les liaisons étant faible, on continuera à parler du système 神 de la double liaison. On fera de même pour le vinylacétylène.

4. Caractéristiques générales des liaisons

Deux cas sont à distinguer: les liaisons localisées et les liaisons délocalisées, c’est-à-dire conjuguées. Correspondant à un nuage électronique répandu sur toute la molécule, les liaisons conjuguées ont perdu leur individualité et le système doit être étudié dans son ensemble (cf. RÉSONANCE [Chimie]).

Les liaisons localisées sont pratiquement indépendantes du reste de la molécule, si bien qu’elles possèdent des caractéristiques à peu près constantes. Le tableau 1 indique les valeurs des deux plus importantes: la longueur et l’énergie, pour quelques liaisons.

La constance des longueurs de liaison A 漣 B dans les molécules permet de définir le rayon de liaison r des atomes par la relation: d ^AB = r ^A + r ^B.

Si les atomes A et B liés ne sont pas de même nature, la densité électronique ne possède plus, comme pour H², le plan médiateur du segment qui est formé par les noyaux comme plan de symétrie. Le nuage électronique est déplacé vers l’un des atomes, A par exemple; on dit que A est plus électro-négatif que B. Mais il importe de préciser que jamais, dans une molécule, on n’aboutira à un déplacement total des électrons avec formation d’ions.

Le centre de gravité des électrons ne coïncidant alors plus avec celui des noyaux positifs, la liaison possède un moment dipolaire . Les moments des diverses liaisons se composent géométriquement pour donner le moment dipolaire total de la molécule.

Une autre caractéristique importante des liaisons est leur polarisabilité 見, c’est-à-dire la facilité avec laquelle elles se déforment sous l’effet d’un champ électrique 劉 extérieur, acquérant l’énergie supplémentaire: 1/2 見 劉². Plus que la polarité liée au moment dipolaire permanent, la polarisabilité (tabl. 2) joue un rôle dans les problèmes de réactivité.

5. Liaisons secondaires

À côté des forces assurant la cohésion des atomes à l’intérieur d’une molécule, on a coutume d’introduire des forces dites secondaires qui s’exercent soit entre les molécules, provoquant des associations plus ou moins stables, soit à l’intérieur même d’une molécule entre atomes non directement liés. En fait, ces forces n’ont pas une origine différente des forces de liaisons. L’intégration rigoureuse de l’équation de Schrödinger relative à l’ensemble de deux systèmes A et B étant impossible, dans la mesure où ces systèmes conservent leur individualité, l’énergie de l’ensemble apparaît comme la somme des énergies des systèmes isolés et d’une énergie que l’on qualifiera d’interaction. Mis en présence l’un de l’autre, les systèmes se déforment mutuellement, leurs fonctions d’onde 切^A et 切^B deviennent respectivement 切^A + 切^A et 切^B + 切^B. Si les modifications 切 sont assez faibles, l’énergie d’interaction apparaîtra comme un développement limité en fonction des divers ordres de déformation. Le premier terme, correspondant aux parties principales 切^A et 切^B des nouvelles fonctions, pourra s’interpréter comme provenant de la simple interaction électrostatique entre les systèmes A et B indépendants. Les autres termes, correspondant à des déformations, seront qualifiés de termes de polarisation. Mais les diverses forces qui en résultent ne sont jamais que des combinaisons des forces de Coulomb entre les noyaux et les électrons, qui sont les seules forces introduites dans l’équation de Schrödinger.

On n’examinera ici que les types d’interaction les plus usuels.

Forces de Van der Waals

L’étude expérimentale des fluides met en évidence des forces responsables des écarts par rapport au fluide parfait à particules indépendantes. Ces forces expliquent, en particulier, le phénomène de liquéfaction.

À leur origine se trouve d’abord, si les molécules sont polaires, l’interaction dite de Keesom: l’énergie d’interaction entre deux molécules identiques de moment dipolaire 猪 est 漣 2/3 ( 猪⁴/k T)r ^-6 (k étant la constante de Boltzmann; T, la température absolue); il en résulte des agrégats de molécules que détruira une élévation de température.

D’autre part, le champ créé par une molécule polaire provoque une déformation des molécules voisines (cf. supra , chap. 4) et l’on peut calculer classiquement l’énergie d’interaction qui en résulte, en introduisant la polarisabilité 見 des molécules. Cette énergie est proportionnelle à 漣 見猪²r ^-6. Les forces qui en résultent sont dites de Debye. Un calcul quantique est cependant préférable.

Mais, à côté de ces forces qui apparaissent seulement entre molécules polaires, sont toujours présentes celles, dites de London, qui proviennent des termes de déformation, d’ordre supérieur. Pour des distances assez grandes, l’énergie correspondante varie encore à peu près proportionnellement à r ^-6.

C’est l’ensemble de ces termes en r ^-6, correspondant par conséquent à une force attractive en r ^-7, qui porte le nom de forces de Van der Waals. Pour les très courtes distances, la force de London devient très grande et répulsive, ce qui se traduit pour les molécules et les atomes par l’existence d’un domaine d’impénétrabilité. Pratiquement, ce domaine, pour les atomes, est une sphère; son rayon est le rayon d’impénétrabilité ou de Van der Waals. Il vaut, par exemple, 0,12 nm pour H, 0,15 nm pour N et 0,20 pour Br.

L’allure de la variation de l’énergie en fonction de la distance entre les deux systèmes est analogue à celle que l’on obtient pour la molécule H². Dans la pratique, on utilise la forme suivante: E = Ar ^-12 漣 Br ^-6. Une telle courbe présente un minimum, correspondant à une position d’équilibre stable. Toutefois, l’énergie mise en jeu est faible (elle est de quelques kilojoules par mole, c’est-à-dire, environ, de 10 à 20 fois inférieure à celle d’une liaison normale), si bien que les associations qui en résultent sont facilement détruites par une élévation de température. On peut citer comme exemple d’associations de Van der Waals les hydrates, les composés d’insertion dans certains cristaux (hélium dans le béryl, hydrocarbures saturés linéaires dans l’urée), les associations entre molécules à l’état gazeux (NO 漣 NO) et surtout les cristaux moléculaires (cf. infra ). Ces forces sont, de plus, responsables du phénomène d’adsorption physique en catalyse hétérogène.

Liaisons hydrogène

Les liaisons hydrogène résultent de l’association entre une molécule A 漣 H et un groupement B porteur d’une paire d’électrons. On les note: A 漣 H ... B. A peut être un atome d’oxygène, d’azote, de soufre, de carbone; B, un oxygène, un azote, un halogène... (cf. infra , LIAISONS CHIMIQUES - Liaison hydrogène).

Forces intramoléculaires

Le fait que les liaisons ne soient pas parfaitement localisées entre les atomes, même dans les molécules non conjuguées, entraîne que l’énergie totale de la molécule n’est pas exactement égale à la somme des énergies des liaisons. Ici encore, on pourra conserver l’approximation de la localisation en introduisant des forces fictives d’interaction intramoléculaires.

L’exemple le plus simple est celui de l’éthane H³C 漣 CH³. L’énergie de la molécule dépend de la position angulaire relative des deux radicaux méthyles, la rotation est dite gênée . La position la plus stable correspond au plus grand éloignement des atomes d’hydrogène. L’étude des stabilités des diverses formes que peut prendre une molécule constitue un des problèmes importants de la stéréochimie ^{[cf. STÉRÉOCHIMIE]}.

6. L’état cristallin

Par abaissement de la température, les diverses particules constituant un gaz ou un liquide s’immobilisent, c’est la solidification. L’état ainsi obtenu est macroscopiquement caractérisé par sa rigidité. Deux cas se présentent: les particules se disposent ou bien au hasard formant un verre ^{[cf. VERRE]}, ou bien dans un ordre déterminé, formant un cristal.

Malgré la diversité apparente des cristaux, il n’y a lieu de distinguer, du point de vue structural, que deux types: les cristaux moléculaires , dans lesquels on retrouve les éléments qui constituaient le liquide, isolés les uns des autres, et qui sont par conséquent formés de molécules de dimensions finies; les cristaux macromoléculaires , formés d’enchaînements périodiques géants.

Dans les cristaux moléculaires, la cohésion entre les molécules est assurée par des forces de Van der Waals (benzène, anhydride carbonique, iode) ou par des liaisons hydrogène (glace). Ces cristaux sont facilement fusibles ou sublimables, et de faible dureté, à cause de la faiblesse des forces de cohésion.

Les cristaux macromoléculaires sont de trois catégories: les réseaux à trois dimensions, comme le diamant ou le chlorure de sodium, qui constituent des molécules géantes; les réseaux à deux dimensions, qui forment des feuillets maintenus entre eux par des forces de Van der Waals ou des liaisons hydrogènes (micas, Cl²Cu); enfin, les réseaux linéaires, formés de fibres réunies par des forces de Van der Waals (tellure) ou des liaisons hydrogènes. Les énergies de liaison entre les divers atomes étant importantes (plusieurs dizaines de kilocalories par mole), les réseaux à trois dimensions sont caractérisés par leur rigidité et leur infusibilité. Dans les réseaux à deux dimensions, au contraire, les feuillets peuvent glisser les uns sur les autres, conférant au cristal un toucher onctueux (talc) et permettant un clivage facile (mica).

La structure des cristaux macromoléculaires est une simple généralisation de la structure moléculaire telle que nous l’avons exposée pour les petites molécules. On aura soit des liaisons localisées, plus ou moins polaires, établies entre atomes convenablement hybridés (diamant, rutile, fluorine), soit des liaisons complètement délocalisées comme dans les métaux. Mais, en aucun cas, il n’existera d’ions au sens strict. Tous les atomes, comme dans une molécule, sont liés les uns aux autres, sans solution de continuité. Par exemple, dans le rutile (TiO²), le titane est lié à six oxygènes (hybridation sp ³d ²), et l’oxygène à trois atomes (hybridation sp ²); dans la fluorine, le calcium est lié à huit atomes de fluor, et le fluor à quatre calcium; dans le chlorure de sodium, chaque atome est lié à six voisins.

7. La nature de la liaison chimique

Si la mécanique quantique permet d’obtenir une description satisfaisante des molécules, le problème de la nature de la liaison chimique reste entier. En effet, par construction, la mécanique quantique ne nous donne qu’une description globale de la molécule. Tout découpage d’une propriété globale en propriétés locales est conventionnelle (cf. chimie QUANTIQUE), en particulier la notion de liaison au sens où l’entend le chimiste. Pourtant, la puissance du concept classique de liaison ne peut pas ne pas correspondre à quelque réalité physique sous-jacente.

Une façon usuelle d’interpréter la fonction d’onde totale utilisée dans la méthode des orbitales moléculaires consiste à dire que les électrons s’associent par paires sur des niveaux moléculaires, étant bien entendu que les électrons s’échangent continuellement entre eux. L’utilisation d’orbitales moléculaires localisées (d’où découle le concept d’hybridation, cf. chimie QUANTIQUE) peut laisser croire que l’on rejoint ainsi le modèle classique des paires localisées entre les noyaux à la précision supplémentaire que les électrons s’échangent entre eux au cours du temps. En fait, il n’en est rien, la localisation des orbitales moléculaires est une opération purement mathématique qui n’implique aucune localisation physique des électrons. Une analyse récente introduit la notion de fluctuation relative du nombre d’électrons présents en moyenne dans des domaines définis, non pas dans l’espace géométrique, mais par les divers couples d’orbitales atomiques hybrides sur lesquels sont construites les diverses fonctions localisées. Pour deux atomes, classiquement considérés comme liés, la fluctuation relative est au plus égale à 0,10. Par exemple, dans CH⁴, entre C et H: 0,06, alors qu’entre deux H (non liés): 0,5. Cette interprétation montre que le concept de liaison au sens classique (domaine dans lequel les électrons séjournent un certain temps par paire) peut être retrouvé, mais à condition de se placer dans un espace autre que l’espace géométrique.

Dans ce modèle, les électrons séjourneraient physiquement pendant un certain temps dans chacun des domaines, s’échangeant sans cesse, le nombre d’électrons dans chacun de ces domaines restant pratiquement inchangé. Cela expliquerait le caractère très local de la plupart des réactions chimiques, que le rôle complètement équivalent que la mécanique quantique fait jouer aux électrons en ne donnant que des caractéristiques moyennes (les mêmes pour tous les électrons) ne permet pas d’expliquer. Appliquée à l’atome, cette analyse justifie la notion d’électrons internes et d’électrons de valence, seuls disponibles pour réagir, étant bien entendu ici encore que, si le nombre d’occupation des divers domaines est bien déterminé, nous ne savons pas nominativement quels électrons s’y trouvent.

Encyclopédie Universelle. 2012.